基于DMD的光场调控
数字微镜器件(DMD)因其同时调控光场复振幅的能力和高速的切换特性,在光场调制领域受到越来越多的关注。相比于液晶相位型空间光调制器(SLM),DMD是一种二值化振幅型空间光调制器。通过与编码算法相结合,将复振幅信息编码到二值化全息图上从而实现对光场振幅和相位分布的动态和精确的波前调控,从而实现调控生成任意的复杂结构光场。为此,我们提出了一种优化的Lee方法,通过引入误差扩散算法进行二值化 提高了计算二值化全息图的精度,实现了在高保真度波前调控的同时还能保持调控生成光场的高空间分辨率。此外,我们提出了一种直接二值化搜索(DBS)的方法来计算高分辨率的全息图用于全息投影显示。

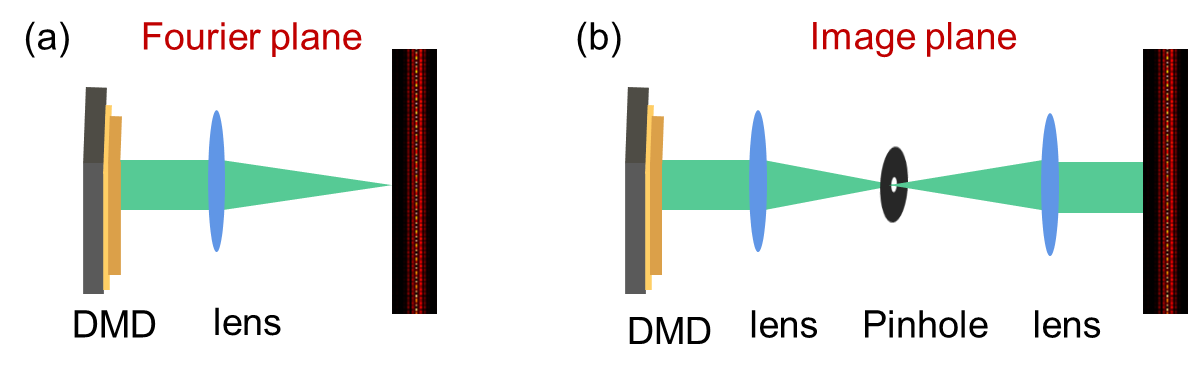
空间光调制器应用于光场调制通常有两种方式,一种是在成像面上直接调制光场的振幅和相位分布,一种是在傅立叶平面上调制光场的频谱分布。DMD也同样适用于这两种调制方式。这两种调制方式的联系在于,频谱面上的高频信息调制对应于成像面上的细节信息调制,反过来也成立。因此,对于理想的可连续调节的空间光调制器件,这两种方式的调制效果是一样的。然而,对于DMD这样的二值化的空间光调制器,其调制精度是有限的。具体在应用中采用哪种调制方式,需要根据不同的需求而定。例如,我们需要生成的复杂光场的振幅函数变化得比较快,此时Lee方法的精度就会下降。但是如果我们编码目标光场的频谱分布就有可能得到比较准确的结果,例如Airy光束的生成最早就是通过调制其频谱实现的。此外,在光场调制实验中DMD表面的不均匀性(Curvature)以及光学系统的像差(Aberration)会影响生成光场的保真度。为此,我们课题组研究了基于DMD的光场调制方式以及系统相差矫正的方法。
结构光场是一类具有特殊时空演化特性的自定义光场。结构光场在光与物质相互作用过程中具有新颖的特性,在光操控、生物医学成像、光学传感和光通信等领域得到了广泛的应用。我们课题组基于DMD和SLM开发了多种光场调控技术,实验上生成了非衍射光束、自加速光束、矢量光束和涡旋光束,并研究了其光场传输特性。
光瓶
传统的高斯光镊无法捕获吸热比较强的微粒,我们提出了一种新型可调控的光瓶,这一类光场具有瓶状的光强分布,其中间光强低,周围光强高,其非均匀强度分布的光场能使吸热比较强的微粒受到光强比较低的位置的光泳力,能够三维稳定地捕获吸热比较强的磁性微粒。我们提出一种基于广义Bessel-Gauss光束的全新的光瓶产生方法。理论上,只需要选择合适的光场参数,这种光束能够自然地形成瓶状的光场结构。通过简单的参数调控,光瓶能够呈现出不同的几何形状,而且光瓶内部空间结构和光强分布都可以连续地调控,这为它在光捕获中的应用提供了新的调控维度[1]。

OAM光束
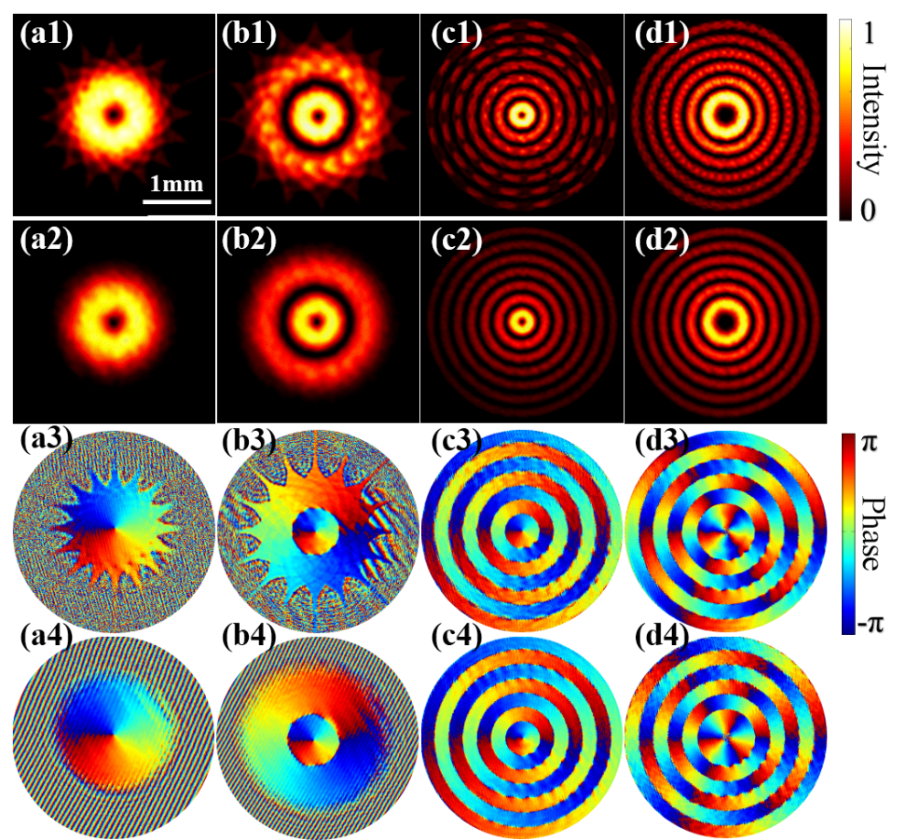
我们提出了一种优化的Lee方法,利用二值化光学元器件DMD实现动态调控生成轨道角动量(OAM)光束。通过引入误差扩散算法进行二值化 提高了计算二值化全息图的精度,实现了在高保真度波前调控的同时还能保持光场的高空间分辨率。为了在实验上验证这一方法,我们首先基于优化的Lee方法调控生成了不同类型的OAM光束。实验结果表明,对于我们所有测试生成的OAM光束,优化的Lee方法的光场生成保真度达到了0.985。因此,优化的Lee方法可以对光场的振幅和相位分布进行准确的调控。此外,我们实验证明了以切换速度高达17.8 kHz的速率动态调控生成了不同的OAM光束,包括纯的OAM模式和混合阶OAM模式[2]。在此基础上,实现了利用复用的OAM模式进行准确的信息编码,本文为采用空间模式编码的高速经典和量子通信提供了途径。
矢量涡旋光束
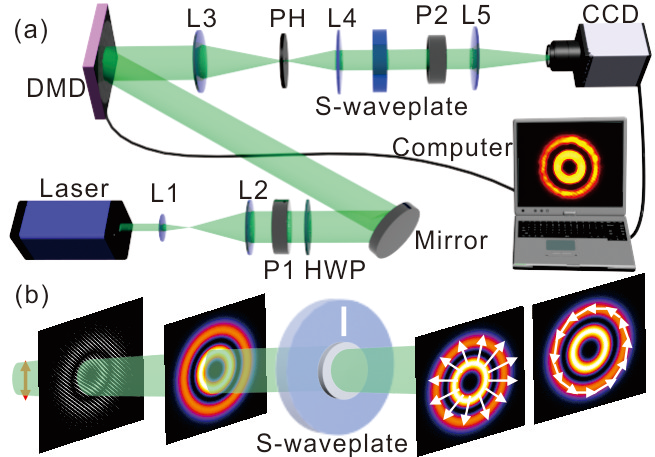
我们提出了一种新的技术,直接将线性偏振高斯光束转换成具有不同空间结构的矢量涡旋光束。 我们首先基于二值化DMD的复振幅调制能力,准确调控生成了不同的拉盖尔-高斯、贝塞尔-高斯和螺旋马蒂厄-高斯光束。进一步,我们将DMD的光场复振幅调制能力和S玻片的偏振调制能力相结合,在实验上有效地将线偏振涡旋光束转换成矢量涡旋光束[3]。此外,所产生的矢量涡旋光束在经过任意偏振操作后仍能保持其偏振分布的空间对称性。

非衍射LG光束
我们利用高径向阶 LG 光束的独特性质,构造了具有准非衍射特性的环形光晶格。准非衍射晶格光束能够自然地形成多个光条带和光学管道,具有超长焦深的特点。通过与 Bessel 光束的比较,我们研究了这一类光束的演化行为。为了验证理论预测的正确性,我们基于DMD 灵活地调控生成了不同横向分布的环形光晶格[4]。此外,还对超长光学通道进行了实验重构。我们的工作为 LG 光束的研究带来了新的视角,所生成的具有独特传输特性的环形光晶格在光学捕获和超分辨率显微成像等领域具有潜在的应用前景。

晶格光片的合成和扫描
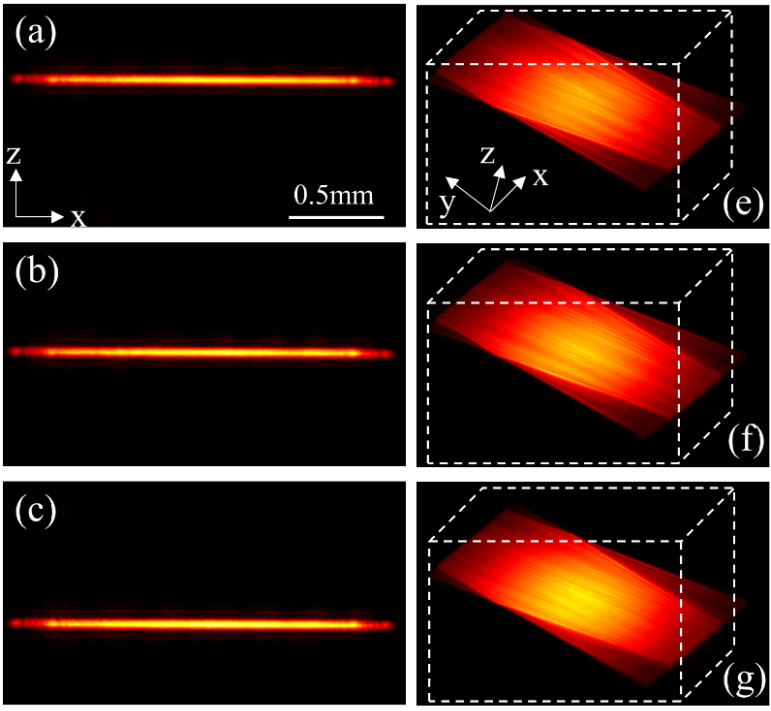
晶格光片显微术由于其在时空分辨率和低光毒性方面的优越性能,在生物医学成像领域中具有非常独特的地位。然而,成像系统通常比较复杂,因为生成晶格光片需要机械扫描和精确的对准。为此,我们提出了一种利用DMD合成和扫描晶格光片的实验方案。 通过充分利用DMD的快速切换和对光场复振幅分布准确调控的能力,我们在实验上通过数字抖动实现了单次生成均匀的晶格光片。 特别地,在没有任何机械运动的情况下,我们也实现了在深度方向对晶格光片的快速扫描[5]。
紧聚焦光场的自旋-轨道角动量相互作用
光同时具有自旋和轨道角动量属性:在傍轴条件下,光的自旋和轨道角动量在自由空间传输过程中是相互独立且各自守恒的;在非傍轴条件下,例如紧聚焦或者散射光场中,光的自旋与轨道角动量之间会发生相互耦合和转化。在这些光学系统中,光的自旋-轨道角动量相互作用(SOIs)会影响聚焦光场的分布和性质,这由入射光的偏振和空间自由度共同决定。特别地,新型光场在紧聚焦条件下表现出独特的SOIs现象。例如,紧聚焦圆偏振光束中的入射自旋角动量(SAM)可以转换成聚焦场的轨道角动量(OAM),也就是发生了自旋-轨道角动量的转化(SOC)。除了SOC以外,轨道引起的局部自旋角动量(轨道-自旋角动量的转化,OSC)也会发生在紧聚焦条件下。紧聚焦光场中可调控的SOIs在光学捕获和光学超分辨显微成像等研究领域具有潜在的应用前景。
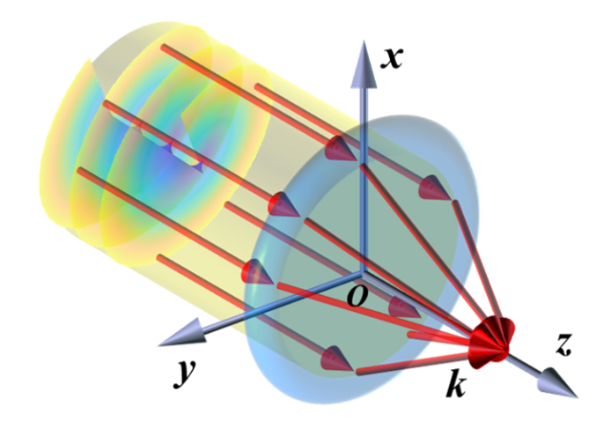
我们通过解析计算在理论上证明了紧聚焦的线偏振涡旋光束在聚焦平面会发生局部的OSC。线偏振光束的入射涡旋相位分布导致聚焦场产生了纵向SAM分布,同时也改变了聚焦场横向的SAM分布。通过分析与SAM密度分布相关的聚焦场偏振态分布发现,水平线偏振涡旋光束聚焦场中局部的纵向SAM的出现归因于入射涡旋相位引起的聚焦场偏振分布的改变。特别地,这种纵向的SAM分布可以通过改变入射OAM的大小和正负以及光场的线偏振方向进行调控[6]。我们的工作增加了对光学自旋-角动量耦合更全面的理解,这种可调节的SAM分布在多功能光操控领域具有一定的应用前景。


进一步,我们从理论上研究了既包含涡旋相位波前和高阶偏振分布的紧聚焦高阶庞加莱球光束中自旋和轨道角动量之间的相互作用,并进一步定量研究了这一类光束自旋和轨道角动量之间的相互转化。研究发现自旋到轨道角动量的转化由入射场的自旋角动量和聚焦系统的数值孔径共同决定。特别地,基于高阶庞阶莱球光束是由左旋圆偏振涡旋光和右旋圆偏振涡旋光叠加而成,我们定义了其SOIs的一般描述,这为在非傍轴条件下任意的SOIs研究奠定了基础。这一发现寄希望于加深对SOIs的理解,SOIs在经典光学和量子光学中都发挥了非常关键的作用[7]。


参考文献:
[1] L. Gong, W. Liu, Q. Zhao, Y. Ren, X. Qiu, M. Zhong, and Y. Li, Controllable light capsules employing modified Bessel-Gauss beams, Scientific Reports 6, 1-12 (2016).
[2] X. Hu, Q. Zhao, P. Yu, X. Li, Z. Wang, Y. Li, and L. Gong, Dynamic shaping of orbital-angular-momentum beams for information encoding, Optics Express 26, 1796-1808 (2018).
[3] L. Gong, Y. Ren, W. Liu, M. Wang, M. Zhong, Z. Wang, and Y. Li, Generation of cylindrically polarized vector vortex beams with digital micromirror device, Journal of Applied Physics 116, 183105 (2014).
[4] Q. Zhao, L. Gong, X.-Y. Hu, P.-P. Yu, Z.-Q. Wang, and Y.-M. Li, Harnessing Laguerre-Gaussian beams to construct quasi-nondiffracting optical ring lattices, IEEE Photonics Journal 10, 1-7 (2018).
[5] Zhao Q, Tu S, Sun H, et al. Motionless synthesis and scanning of lattice light sheets with a single digital micromirror device[J]. Applied Physics Letters 120, 211106 (2018).
[6] P. P. Yu, Q. Zhao, X. Y. Hu, Y. M. Li, and L. Gong, Orbit-induced localized spin angular momentum in the tight focusing of linearly polarized vortex beams, Optics Letters 43, 5677-5680 (2018).
[7] P. P. Yu, Y. F. Liu, Z. Q. Wang, Y. M. Li, and L. Gong, Interplay between Spin and Orbital Angular Momenta in Tightly Focused Higher-Order Poincare Sphere Beams, Annalen Der Physik 532, 2000110 (2020).


